Importance Of Time Value Of Money

Time value of money is defined as "the value derived from the use of money over time as a result of investment and reinvestment". Time value of money means that "worth of a rupee received today is different from the worth of rupee to be received in future". The preference for money now, as compared to future money is known as time preference of money.

The whole set of financial decisions (whether financing decision or investment decision) hinges on the fact that the value of one rupee today is not equal to the value of one rupee at the end of one year or at the end of second year. In other words, we cannot assume that the value of rupee remains the same. This is known as 'Time Value of Money'.

'Time Value of Money' signifies that the value of a sum of money received today is more than its value receivable after some time.

Time value of money principle also applies when comparing the worth of money to be received in future and the worth of money to be received in further future. In simple words, TVM principles says that the value of a given sum of money to be received on a particular date is more than the same sum of money to be received on a later date.

Contents

1. An Overview of Time Value of Money
2. Introduction to Time Value of Money
3. Meaning of Time Value of Money
4. Concept of Time Value of Money
5. Time Value of Money – Concepts: Explanation, Calculation and Examples (With Time Period)
6. Top 4 Importance of Time Value of Money
7. 4 Major Reasons Why People Have Time Preference for Money?
8. Top 5 Reasons as to Why People Have Time Preference for Money
9. Relevance of Valuation of an Enterprise
10. Top 2 Techniques for Estimating Time Value of Money – Discounting and Compounding Technique (With Methods for Calculation Future Value and Comparison)
11. Formula for Calculating Present and Future Value of Money (With Differential Equations)
12. Valuation – Concepts: Book Value, Market Value, Liquidation and More…
13. Valuation of Bonds, Debentures, Preference and Equity Shares
14. 2 Important Concept of Rate of Interest: Simple and Compound Interest Rate (With Comparison)
15. Theory of Interest (With Equation)
16. Practical Applications of Time Value of Money
17. Timeline
18. Annuity in Time Value of Money – Meaning, Types and Methods for Calculation
19. Annuity: Meaning, Example, Practical Uses and Examples
20. Types of Cash Flows: Perpetuity, Annuity Due,  Growing Perpetuity and Growing Annuity
21. Risk – Meaning, Types and Measurement
22. Return – Meaning and Measurement
23. Time Value Factors (TVFS)
24. Capital Asset Pricing Model: Meaning, Equation and Assumptions
25. Time Preference Rate (TPR)
26. Multiple Choice Questions and Answers

Time Value of Money in Financial Management: Meaning, Importance, Reasons, Techniques, Valuation, Annuity, Formula, Examples, Applications and MCQs

Time Value of Money – An Overview

Time value of money is singularly important amongst all the concepts and principles used in the field of financial management. Crux of time value concept is that money has a time value. A rupee to be received a year from now is not worth as much today as a rupee to be received immediately. At Least three factors contribute to the time value of money.

First, there is the simple bird-in-the-hand notion that uncertainty increases with die futurity of an event so that the promise of one rupee in 10 years is usually worth less than a similar promise in one year. This bird-in-the-hand principle is extremely significant in making investment decisions.

Second, under inflationary conditions, purchasing power of the rupee over time declines. So if inflation is expected to continue, future rupees will have a depreciated value compared to current value.

Third, there are opportunity costs associated with any expenditure, which again makes future rupees less valuable than the current ones. Opportunity costs arise because a rupee today can be profitably invested and as a result will be worth more than a rupee in the future.

Opportunity costs are not losses in the absolute sense but they are relative to what could have been, had the decision maker made the best use of available resources. By opting for use of resources over another, a decision maker always incurs an opportunity cost equal to the income that could have been earned on the next best alternative.

Time value of money is based on the premise that cash flows occur at different points of time. As such, Time Lines constitute an important ingredient of time value of money.

Time Value of Money – Introduction

The recognition of time value of money in financial decision making is extremely important. Maximisation of shareholder's welfare is the basic objective of the financial management, is superior to profit maximisation because, among other things the former incorporates the timing of benefit received, while he later ignores it.

This requires the financial management to take appropriate decisions on financing, investment and dividends. While taking these decisions the financial management must keep the "time factor" in mind, eg.

(i) When interest on funds raised will have to be paid

(ii) When return on investment will be received

(iii) Whether it will be received on a consistent basis or otherwise etc.

All this requires that the finance manager knows about the various valuation concepts, viz compound value concept, annuity concept, present value concept etc.

All those concepts are basically based on this fact that the money has a time value i.e. a rupee today is much more valuable than a rupee tomorrow.

Time Value of Money – Meaning

Time value of money is defined as "the value derived from the use of money over time as a result of investment and reinvestment". Time value of money means that "worth of a rupee received today is different from the worth of rupee to be received in future". The preference for money now, as compared to future money is known as time preference of money.

"Time value of money means that the value of a sum of money received today is more than its value received after some time", conversely the sum of money received in future is less valuable than it is to-day.

In other words, the present worth of rupee received after some time will be less than a rupee received today. The Time value of money can also be referred to as "time preference for money". This then constitutes the rationale of considering time value of money in financial decision making.

Time Value of money is the concept that the value of a rupee to be received in future is less than the value of a rupee on hand today. One reason is that money received today can be invested thus generating more money.

Another reason is that when a person opts to receive a sum of money in future rather than today, he is effectively lending the money and there are risks involved in lending such as risk and inflation. Default risk arises when the borrower does not pay the money back to the lender. Inflation is the rise in the general level of prices.

Time value of money principle also applies when comparing the worth of money to be received in future and the worth of money to be received in further future. In simple words, TVM principles says that the value of a given sum of money to be received on a particular date is more than the same sum of money to be received on a later date.

Time value is a concept that recognizes the relevant worth of future cash flows arising as a result of financial decisions. Money loses its value over time which makes it more desirable to have it now rather than later.

Concept of Time Value of Money

The whole set of financial decisions (whether financing decision or investment decision) hinges on the fact that the value of one rupee today is not equal to the value of one rupee at the end of one year or at the end of second year. In other words, we cannot assume that the value of rupee remains the same. This is known as 'Time Value of Money'.

The recognition of time value of money in financial decision-making is extremely important. A financial decision taken today has implications for a number of years. Every financial decision involves the comparison of cash outflow (outlays or cost of investment) and cash inflows (benefits or earnings after tax but before depreciation). For a meaningful comparison, the two sets of flows must be strictly comparable.

One basic requirement of comparability is the incorporation of time elements in calculations. To put it in another way, in order to have a logical meaningful comparison between cash flows that accrue in different time periods, it is necessary to convert the sums of money to common points in time. If the timing of cash flows is not considered, the firm may take decisions which may fail its objectives.

'Time Value of Money' signifies that the value of a sum of money received today is more than its value receivable after some time.

This may be due

(i) risk, i.e., uncertainty associated with future receipts or

(ii) inflation causing the decline in purchasing power of money or

(iii) reinvestment opportunities for funds received early.

It can be argued that the risk element associated with future receipt of money could be eliminated or reduced to a greater extent through suitable promises, insurance against default, etc., so that possibility of default (money not to be received in future) becomes quite remote.Naturally, the time value of money then becomes irrelevant.

Similarly, if it is assumed that the economy is free from inflation, then the value of money today and that of tomorrow may be taken to be the same and in this case also time value of money becomes irrelevant.

In spite of these two extreme assumptions, a rupee of today would be preferred to a rupee of tomorrow (i.e., future) because the rupee received today may be invested and its value tomorrow (in future) would be more (this is due to the fact that the rupee invested will fetch some interest).

It is only with respect to reinvestment opportunities of funds received early that future cash flows are taken to be less valuable than the present ones. Funds received today would earn a rate of return which may not be possible in case they are received later.

Time value of money is expressed generally in terms of a rate of return or as discount rate. Understanding the time value of money essentially involves the understanding of the concepts of compounding and discounting in mathematical terms. These concepts are inherent in financial decisions of any nature.

Time Value of Money – Concepts: Explanation, Calculation, Formula  and Examples (With Time Period)

The concept of time value of money is very fundamental to financial decision making. Any decision which ignores this basic concept is sure to lead to wrong decisions. This concept is often known as the 'Discounting Principle' also. This is of great significance in any decision where the operations are stretched over a period of time, or where we have to make intertemporal choices.

The concept of time value of money tells us that the value or real worth of any sum of money is dependent on, 'the point of time when it is received or paid'? The worth of any sum is greater if it is received at present, than if the same sum is to be received at some future date.

Similarly, we would prefer to pay any sum in future than paying it now, because paying now is more burdensome, and paying the same sum in future makes the burden lighter.

The concept of time value of money is based on the premise that lending opportunities always exist and interest rate is positive. It means that if we receive any sum of money at present, we can always lend it and earn some interest in future.

In this way, this amount will become greater than the same sum of money which is to be received at a future date. In other words, we can say that the amount to be received in future has lower worth than the amount to be received now. This is called discounting of the future.

The discounting of the future is done for the time gap between the present and the future and the more distant the future, the greater shall be the extent of discounting. Thus, discounting bridges the gap between the present and the future, and this is done at the prevailing rate of interest and that too at the compound rate.

The whole process can be explained as follows:

Suppose the rate of interest is 10 percent per annum.

If we receive a sum of Rs. 500 now, it will earn an interest of Rs. 50 in one year and will become equal to Rs. 550 after 1 year. The same sum will earn an interest of Rs. 55 in the second year and will become equal to Rs. 605 after two years. How this money grows at different points of time can be calculated by the following compound interest formula?

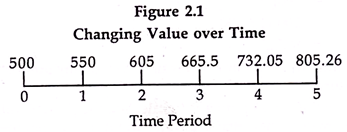
In the above figure, different values are given at different time periods. These are all values of the same Rs. 500 at different points of time, assuming the rate of interest to be 10 percent per annum. The amount of Rs. 500 becomes Rs. 550 after one year, 605 after two years and 805.26 after 5 years. In terms of valuation all sums have equal value.

All these values have been calculated by the above mentioned compound interest formula. This, well known compound interest formula, can be modified a little to make our working more convenient. Instead of using 'r' as rate percent, we use the symbol 'i' to indicate rate per rupee.

Accordingly, the modified formula would be:

Suppose, a sum of Rs. 500 is to be received after 4 years and we have to find its present worth or present value, we can find it as follows (assuming the same rate of interest).

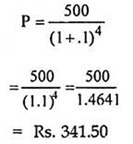
Hence, we can say that the discounted value of Rs 500 payable/receivable after 4 years is Rs 341.50. In this manner, we can find the discounted value of any sum of money payable/ receivable at some future date.

Compounding and discounting are the two sides of the same coin. If present values are carried into the future, it is called 'compounding' and if future values are transferred into present, it is called 'discounting'. Obviously, compounding increases the value, while discounting decreases the same. Both are the consequences of the same concept i.e. 'time value of money'.

It would now be obvious to the readers, that the compounding or discounting impact is dependent on time period and the interest rate or the discount rate. If the discount rate is high, there is a greater reduction in value and vice versa.

For example, in the above example if the interest or the discount rate is taken as 12 percent, then the present value of Rs 500 payable/ receivable after 4 years would be

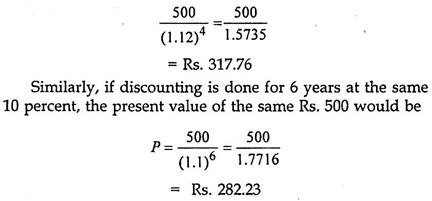
This value is lower than what we get when it is discounted for 4 years only.

In this manner, discounted values can be found for different rates and time periods.

Time Value of Money – Top 4 Importance

In the financial decisions, the time value of money holds great importance. It is now the most significant principle in finance and economics. There are certain valid reasons for this state of affairs.

Few are:

Importance # (i) Inflation

Because of inflationary conditions, the rupee today has a higher purchasing power than rupee in future. As a result, those who have to receive the money prefer to receive the same as early as possible, while those who have to pay the money try to delay the payment.

Importance # (ii) Uncertainty

Since the future is characterised by uncertainty, individuals/business concerns prefer to have current income rather than having the same payment at a later date. They have an apprehension that the party making the payment may default due to insolvency or other reasons.

Importance # (iii) Preference for Present Consumption

Both due to uncertainty and inflationary condi­tions, individuals prefer the consumption to future consumption. They do not wish to save for the future by curtailing current consumption.

Importance # (iv) Opportunities for reinvestment

Money can be employed to generate real returns. Individual's business concerns reinvest the money at a certain rate so as to have some yield on it.

As such a financial manager of any business concern cannot ignore the concept of time value of money while making any financial decisions, otherwise his decisions will be invalid and incorrect also.

Time Value of Money – Significance in Financial Decision Making

The recognition of the time value of money is extremely significant in financial decision making because, most of financial decisions such as the acquisition of assets or procurement of funds, affect firm's cash flows in different time periods, for example, if a fixed asset is purchased, it will require an immediate cash outlays and will affect cash flows during many future periods.

Similarly if the firm borrows funds from a bank or from any other sources, it receives cash now and commits an obligation to pay interest and return principal sum in future. While taking decisions on these matters, the financial management must keep the time factor in mind.

If the timing of cash flows is not considered, the firm may make decisions which may falter its objective of maximising the owner's welfare.

Time Value of Money – 4 Major Reasons Why People have Time Preference for Money?

The major reasons for time preference of money are:

Reason # 1) Preference for Consumption:

Most people have preference for present consumption over future consumption of goods and services either because of the urgency of their present wants or because of the risk of not being in a position to enjoy future consumption that may be caused by illness or death, or because of inflation.

Reason # 2) Investment Opportunities:

Most individuals prefer present cash to future cash because of the available investment opportunities to which they can put present cash to earn additional cash.

For example, an individual who is offered Rs. 5000 now or Rs. 5000 one year from now would prefer Rs. 5000 now if he could earn on it an interest of, say, Rs. 500 by putting it in the savings account in a bank for one year. His total cash in one year from now will be Rs. 5500.

Reason # 3) Future Uncertainties:

One of the reasons for preference of current money is that there is a certainty about it whereas the future money has an uncertainty. There may be chances that the other party (the creditor) may become insolvent.

Reason # 4) Inflationary Economy:

In an inflationary economy, today's rupee has more purchasing power to buy, rather than the same amount of money can buy at a later date.There is a preference of having money at present over at a future point of time.

This means that:

a. A person will have to pay in future more for a rupee received today; and

b. A person may accept less for a rupee to be received in future.

Top 5 Reasons as to Why People Have Time Preference for Money

Individuals generally prefer possession of a given amount of cash now rather than the same at some future time is known as 'Time Preference for Money'.

There are varied reasons for time preference for money.

The important reasons as to why people have time preference for money are as under-

(a) Availability of better investment opportunities.

(b) Due to Risk and uncertainty of Cash flows.

(c) Due to Inflationary Conditions.

(d) Preference for Present Consumption of goods, commodities and services.

(e) Due to Urgency or Emergency.

A brief description of each of the above is given below:

Reason # (a) Availability of Better Investment Opportunities:

There are investment opportunities, where people can invest their cash and earn some interest or return through lending or investment. A rupee invested today is more valuable than a rupee invested tomorrow, so they prefer to receive money today than to receive the same tomorrow

Reason # (b) Due to Risk and Uncertainty of Cash Flows:

Future is uncertain with plenty of risks. In this environment cash outflows (i.e., investment made at '0' period) are in investors control but the cash inflows (i.e. incomes earned from investments) return on investment and recovery of investments are not in investor's control. The receipt from outsiders is uncertain. Hence, the investors prefer to receive cash now rather than receiving the same in future.

Reason # (c) Due to Inflationary Conditions:

In the inflationary condition the purchasing power of money is decreasing. In this condition a rupee today has more purchasing power than a rupee tomorrow. So people prefer to receive cash now rather than tomorrow.

Reason # (d) Preference for Present Consumption:

It is human tendency to prefer present consumption of goods, commodities and services; than to postpone their consumption to future periods. Hence people prefer to possess cash for current consumption, rather to postpone or cancel.

Reason # (e) Due to Urgency/Emergency:

People prefer to receive cash today than in some future date, to meet some urgent needs or to meet emergency requirements.

Time Value of Money – Relevance of Valuation of an Enterprise

So as to maximize the firm's value, it must choose the best combination of decisions in respect of investment, financing and dividends. These decisions have return-risk complexions which, in turn, affect the value of the firm. More specifically, the question of valuation arises in a large number of situations.

Thus, the principle of valuation is closer to determining when the management is contemplating whether to acquire an enterprise or merger issue is under consideration, it needs to employ relevant concepts and techniques of valuation to assess new investment opportunities and to determine the value of an entire firm involved in a merger. Likewise, feasibility of a reorganization plan can be studied by determining the value of the enterprise.

A finance manager plaguing the problem of recapitalisation makes extensive use of principles of valuation. In the same vein, principles of valuation are useful to the management who is interested to know the realizable value of the enterprise being terminated either due to bankruptcy or voluntary liquidation. In analyzing utility of leases, a finance manager employs very frequently the principles of valuation.

In addition, a firm considering a public offering of its own stock to raise equity capital is faced with the need to establish a price for the issue. The question of value to be placed on a going business either as a whole or on a fraction thereof also comes upon in the purchase, sale, taxation and pledge of existing securities.

Thus, concepts and principles of valuation constitute vital cornerstones of financial management, thorough understanding of which is imperative for reaching prudent decision making.

Three major aspects of valuation that pervade financial decision areas are time value of time, valuation of long-term securities and risk and return.

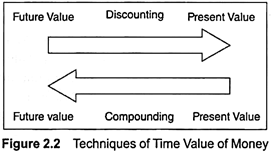
Top 2 Techniques for Estimating Time Value of Money – Discounting and  Compounding Technique (With Differences and Methods for Calculating Future Value and Comparison)

There are two techniques of estimating time value of money which are shown in figure 2.2 and explained as follows:

1. Discounting Technique or the Present Value Method

2. Compounding Technique or the Future Value Method

Technique # 1. Discounting or Present Value Method:

The current value of an expected amount of money to be received at a future date is known as Present Value. If we expect a certain sum of money after some years at a specific interest rate, then by discounting the Future Value we can calculate the amount to be invested today, i.e., the current or Present Value.

Hence, Discounting Technique is the method that converts Future Value into Present Value. The amount calculated by Discounting Technique is the Present Value and the rate of interest is the discount rate. Discounting can be done a number of times and based on this, methods for calculating Present Values are listed as follows in Table 2.2 –

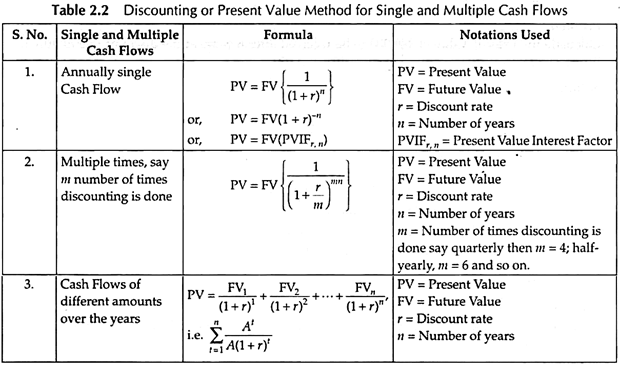
Technique # 2. Compounding or Future Value Method:

Compounding is just the opposite of discounting. The process of converting Present Value into Future Value is known as compounding.

Future Value of a sum of money is the expected value of that sum of money invested after n number of years at a specific compound rate of interest.

Methods for calculating Future Value are given as follows Table 2.3 –

Difference between Compounding and Discounting Methods:

The points of differences between compounding and discounting are as follows:

Difference # Compounding:

i. The process of converting the Present Value into Future Value is known as compounding.

ii. Interest rate is used to calculate the Future Value or the compounded value.

iii. Higher the interest rate greater will be the future or the compounded value.

iv. Future Value is always greater than the Present Value provided the interest rate is positive –

FV = PV (1 + r)n

Difference # Discounting:

i. The process of converting Future Value in Present Value terms is known as discounting.

ii. Discount rate is used to calculate the Present Value.

iii. Higher the discount rate lower will be the Present Value.

iv. Present Value is always less than the Future Value –

Every finance manager has to take three important Financial Management decisions such as – the Investment Decision, Financing decision and the Dividend decision. Finance manager has to take all these decisions keeping in mind the value maximisation or the wealth maximi­sation objective of Financial Management.

So a finance manager before taking a financial decision should keep in mind the objective of value maximisation. In case of an Investment Decision, where return is fixed and assured it is said to be risk-free investment, for example, 10% Reserve Bank of India Bonds, government bonds, keeping money in deposit accounts offered by public sector banks, etc. In this case, the probability of the return is 1 and hence no risk is associated with it.

Again for taking Investment Decisions for investing in shares of a company, the risk associated with mutual funds needs to be considered as in this type of investment the return varies which is neither fixed nor assured.

Share market is volatile and the return varies depending on certain macro level factors and company-specific factors such as – capital depreciation, fluctuating dividend rate due to profit fluctuation, fund crisis, etc.

So, two aspects are involved in any financial decision—one the risk and another return. Both these two factors vary from one decision to another. A proper balance or trade-off between risk and return is required to maximise the return by minimising the risk and, thereby, achieving the goal of maximising the market value to shares.

Time Value of Money – Formula for Calculating Present and Future Value of Money (With Differential Equations)

A. Present Value:

1. Present Value of a Future Sum:

The present value formula is the core formula for the time value of money; each of the other formulae is derived from this formula.

For example- the annuity formula is the sum of a series of present value calculations.

The Present Value (PV) formula has four variables, each of which can be solved for

2. Present Value of an Annuity for n Payment Periods:

In this case the cash flow values remain the same throughout the n periods. The present value of an annuity formula has four variables, each of which can be solved for –

3. Present Value of a Growing Annuity:

In this case each cash flow grows by a factor of (1+g). Similar to the formula for an annuity, the present value of a growing annuity (PVGA) uses the same variables with the addition of g as the rate of growth of the annuity (A is the annuity payment in the first period). This is a calculation that is rarely provided for on financial calculators.

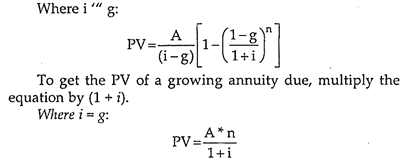
4. Present Value of a Growing Perpetuity:

When the perpetual annuity payment grows at a fixed rate (g) the value is theoretically determined just as to the following formula. In practice, there are few securities with precise characteristics, and the application of this valuation approach is subject to various qualifications and modifications.

Most importantly, it is rare to find a growing perpetual annuity with fixed rates of growth and true perpetual cash flow generation. Despite these qualifications, the general approach may be used in valuations of real estate, equities, and other assets.

This is the well-known Gordon Growth model used for stock valuation.

Present Value of Perpetuity:

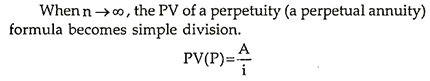
B. Future Value:

1. Future Value of a Present Sum:

The Future Value (FV) formula is similar and uses the same variables.

FV = PV. (1 + i)n

2. Future Value of an Annuity:

3. Future Value of a Growing Annuity:

Derivations:

1. Annuity Derivation:

The formula for the present value of a regular stream of future payments is derived from a sum of the formula for future value of a single future payment where C is the payment amount and n the period.

A single payment C at future time m has the following future value at future time n-

2. Perpetuity Derivation:

Without showing the formal derivation here, the perpetuity formula is derived from the annuity formula.

Specifically, the term-

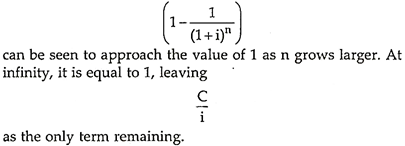
Differential Equations:

Ordinary and partial differential equations —equations involving derivatives and one variable are ubiquitous in more advanced treatments of financial mathematics.

While time value of money can be understood without using the framework of differential equations, the added sophistication sheds additional light on time value, and provides a simple introduction before considering more complicated and less familiar situations. This exposition follows.

The fundamental change that the differential equation perspective brings is that, rather than computing a number one computes a function. This function may then be Analyzed – how does its value change over time – or compared with other functions.

For an instrument whose payment stream is described by f(t), the value V(t) satisfies the inhomogeneous first-order ODE LV = f this encodes the fact that when any cash flow occurs, the value of the instrument changes by the value of the cash flow. The standard technique tool in the analysis of ODEs is the use of Green's functions, from which other solutions can be built.

This formalizes time value of money to future values of cash flows with varying discount rates, and is the basis of many formulas in financial mathematics, such as the Black-Scholes formula with varying interest rates.

Time Value of Money – Valuation – Concepts: Book Value, Market Value, Liquidation and Capitalized Value

Valuation means 'worth' or value of financial security to the buyer. If a security meets his expectations then the security is valuable for him and he will invest in that security, but if the returns expected from the security are less than the price of the security then he will not go for it. Generally, there are two types of assets i.e. physical and financial. Land, building, stock etc. are the examples of physical assets.

Financial assets refer to equity shares, preference shares, bonds etc. Therefore, the concept of the valuation discussed here is related to the valuation of equity shares, preference shares, bonds etc. Present value is the most valid concept of value. There are many concepts to value a financial asset or security.

Different concepts used for different purposes, are being discussed below:

1. Book Value Concept:

Book values are the historical values firm. Assets are recorded on the basis of written down values if these are depreciable assets and in case of intangibles asset value is calculated by deducting amortised value from its acquisition price.

Book value of debenture is shown at its outstanding amount and book value of equity share is the net worth divided by number of shares. However, the book value concept is a historical concept and it doesn't tell the true value of the security.

2. Going Concern Concept:

This is the value received by the seller of a business when he sells his business in running and operating condition. It shows the future value of assets of the business. This may be more or less than the book value of an asset.

3. Market Value Concept:

Market value of a security is the current price at which security can be sold in the market. Market price of a security can be more than the book value of the security if the firm is expected to earn high profits in the future. Market value of a security is equal to its intrinsic value in case the capital markets are efficient.

4. Liquidation Value Concept:

This is the value that a security will have at the time of termination/liquidation of the business. This value may be lower than the market value as the business has come to an end.

5. Capitalized Value Concept:

This is the sum of present value of cash flows from a security discounted at the desired rate of return. The desired rate of return depends upon the risk level of the security. Higher the risk associated with security, higher would be the discount rate at which the security will be discounted. Discount rate consists of the risk free rate of a security and its risk premium.

Time Value of Money – Valuation of Bonds, Debentures, Preference and Equity Shares (with Examples, Types and Methods)

The basic objective of the financial management is to enhance the market value of the securities of the firm. There is thus a need to develop a valuation model for the firm to identify the variables which influence the value of securities.

a) Valuation of Bonds or Debentures

Meaning and Definitions of Bond or Debenture:

The term "debenture" has been derived from Latin word "Debere" which means to owe a debt. Debenture means a document which either creates a debt or acknowledges it, and any document which fulfills either of these conditions is a debenture.

Debenture may be defined as a document issued by the company as an evidence of debt. It is the acknowledgement of a company's indebtedness to its holders.

In the words of Evelyn Thomas "It is a document under the company's seal which provides for the payment of a principal sum and interest thereon, at regular intervals which is usually secured by fixed or floating charges on the company's property or undertaking which acknowledges a loan to the company".

The valuation of bonds or debenture is relatively easy.

In order to understand the valuation of bonds or debentures, it will be useful to study the meaning of the following terms:

1) Par value:

This is the value stated on the face of the bond. It represents the amount the firm borrows and promises to repay at the time of maturity. Usually a debenture or bond has a face value of Rs. 100, sometimes it is Rs. 1000 also.

2) Coupon rate and Interest:

The debenture or bond carries a specific interest rate which is called the coupon rate. Interest is payable at this rate on the face value of the debenture or bond. However if the debenture holder has not paid the full face value of the debenture, he will be paid interest only on paid up value.

3) Maturity period:

Maturity period reference to the period after which the money raised on account of debenture or bonds will be repaid to the debenture holders.

4) Types of Debentures or Bonds:

Debentures or Bonds are of two types:

I) Redeemable debentures

II) Irredeemable debentures.

Basic Debenture of Bond valuation models or Debentures

I) Determination of present value of Redeemable Bond or Debenture:

Debentures are usually issued on the condition that they shall be redeemed after a certain period. Such debentures are known as redeemable debentures.

As it is stated above that a debenture holder is entitled to get the following amounts:

i) Interest at a fixed rate till maturity and

ii) The Principal amount of the debenture on its maturity.

The value of a debenture is therefore equivalent to the present value of the annual interest payments plus the present value of principal payable at the time of maturity.

This can be put in the form of following equation :

Vd = 1 (ADF1) + F (DFF)

Where: Vd = Current value of the debenture or bond

I = Interest payable on the bond

ADFI = Annuity discount factor applicable of interest

(at the required rate of interest)

DFF = Appropriate discount factor applicable to face value

(at the required rate of interest.)

F = Face value.

Example:

A debenture of Rs. 100, bearing an interest rate of 15 percent will mature for repayment after 5 years, The required rate of return on this debenture is 10% calculate the current value of the debenture.

Solution: In order to calculate the current value of the debenture it will be necessary to find out the following two discount factors.

a) Appropriate discount factor for annual interest (ADFI) payment (i.e' at 10% for 5 years). The annuity table gives this factor as 3,791.

b) Appropriate discount factor for face value (DFF) to be received after five years at the required rate of return i.e. 10%. The Present value table gives this factor as 0.621.

The value of the debenture can be ascertained as under:

Vd = I (ADFI) + F (DFF)

= 15 (3.791) + 100 (0.621)

= 56.865 + 62.10

= 118.965 or Say Rs. 119.

II) Valuation of perpetual or irredeemable Bonds or Debentures

These debentures are not repayable during the lifetime of the company. When the company goes into liquidation, they become redeemable. They also become redeemable in case of serious default on the part of the company viz. Non payment of interest.

The value of such a debenture or bond can be found out by dividing the amount of interest with the expected rate of return on the investment.

b) Valuation of preference Shares

Preference shares are those shares which carry a preference both regarding dividend and return of capital. The rate of dividend on preference shares is fixed, hence their valuation can be done on the same basis as that of debentures of bonds.

Types of preference Shares:

Preference Shares may be of two types:

i) Redeemable preference Shares.

ii) Irredeemable preference Shares.

i) Redeemable preference Shares:

In the case of redeemable preference shares, the company undertakes to return the amount paid on preference after a certain period of time. In case of these shares the value of shares would be equivalent to the present value of annual dividend plus the present value of amount payable on maturity.

ii) Irredeemable preference Shares:

Irredeemable preference shares constitute permanent capital of the company. These shares cannot be refunded before the winding up of the company. The value of such preference shares can be found out by simply dividing the annual dividend with current yield.

c) Valuation of equity Shares

Shares which are not preference shares are known as equity shares, or ordinary shares. These shares do not carry a fixed dividend rate as is the case with preference shares. Equity shareholders may or may not get dividends. Hence there is greater uncertainty regarding future streams of cash flows in the form of dividend.

The valuation of equity shares is difficult as compared to the valuation of debentures or preference shares, this is because of the following reasons:

i) Equity shares do not carry a fixed rate of dividend or interest.

ii) Unlike a debenture an equity has no definite maturity period.

iii) Earnings or dividends on equity shares are expected to grow unlike interest on debentures and preference dividend.

Methods of Valuation of Equity Shares

Several approaches to calculating the real value of equity shares have been proposed.

They are basically based on two approaches:

1) Dividend capitalisation Approach

2) Earning capitalisation Approach

1) Dividend Capitalisation Approach:

According to this approach the value of an equity share is equal to the present value of dividend expected from its ownership plus the present value of the re-sale price expected when the equity shares are sold.

The approach is based on the following assumptions:

i) Dividend is paid annually

ii) The first dividend is received one year after the equity share is bought and

iii) The re-sale of the equity share accrues at the end of a year.

I) Single period valuation model:

Under this model it is presumed that the investor expects to hold the equity share for a year only. In such a case the value of equity share for him will be equivalent to the present value of dividend at the end of the year, plus the present value of the price he expects to receive on selling of the shares.

II) Multi period Valuation model:

Since equity shares have no maturity period. They may be expected to bring a dividend stream of infinite duration. The value of an equity share is therefore equivalent to the present value of its future stream of dividends.

The value of an equity share can be ascertained by dividing the expected dividends per share by the capitalisation or expected dividend rate.

Growth in Dividends

In the above example, we have presumed that dividends that remain constant are unrealistic. The earnings and dividends of most companies grow over time, at least, because of their retention policies. As a result of this the company would have an increased earning per every year if the number of shares does not change.

i) Share Valuation with Constant Growth in Dividend:

Most share valuation models are based on the assumption that dividends tends to increase over time, this means that the dividend at the end of the first year will be:

D1 = DO (1+g)1

Similarly dividend at the end of Second year will be :

D2 = DO (1+g)2

D2 = D1 (+g) and So on

ii) Share valuation with variable growth in Dividend:

The dividend of a company may not grow at a constant rate. There are companies whose dividends grow at a supernormal growth rate during the periods when they are experiencing very high demand for their products and then, the dividends grow at a normal rate when the demand reaches the normal level.

In order to value equity shares of such companies the following steps may be taken:

1) Specify the amount of dividend receivable for different years during the initial period of supernormal growth.

2) Find out the present value of dividend computed under (1) above at the capitalisation rate by applying discount factors from the present value tables.

3) Apply the normal growth rate to the dividend received for the last year of supernormal growth period to compute the expected dividend for the first year of normal growth period.

4) Find out the present value of the market price of the shares by applying the P.V. factor to the market price computed under point (3) above.

5) Add the present two values : (a) the present value of dividends computed under point (2) and (b) the present market value of shares computed under point (4) above.

6) The resultant figure is the desired present value of shares.

2) Earnings Capitalisation Approach

Calculation of the real value of equity share is basically based on two approaches,

(i) Dividend capitalisation approach

(ii) Earning capitalisation approach.

The dividend capitalisation model as explained in the preceding pages, is the basic share valuation model under this approach The value of an equity share can simply be determined by capitalising the expected earnings.

a) When earnings of the firm are stable.

b) When there is no growth but simply there is only expansion situation.

a) When the earnings of the firm are stable:

In this case earnings will not grow. This happens when the firm does not employ any external financing, nor retains the earnings. In other words, both the growth rate and the retention rate are "zero". In such a case the earning rate and the dividend rate are the some.

b) When there is no growth but simply there is only expansion situation:

The second case in which market value is the capitalised value of the expected earnings is the expansion situation. The firm will grow in the real sense, when it has investment opportunities which will generate earnings of the internal rate of return "(r)" greater than the equity capitalisation rate, "(Ke)". In other words "r" should be greater than Ke. In case r = Ke there is an "expansion" situation but not a "growth situation.

Time Value of Money – 2 Important Concept of Rate of Interest: Simple and Compound Interest Rate (With Formulas and Comparison of Simple and Compound Interest)

The concept of rate of interest are as follows:

1. Simple Interest Rate

It is the rate of interest (percentage) on the actual principal amount. Simple Interest in absolute terms = P x r x n

Where, P = Principal, r = Rate of interest in decimal, n = Number of years

2. Compound Interest Rate

The interest accrued on the previously earned interest is basically Compound Interest. When interest is earned on the interest received previously and the original principal amount, it is known as Compound Interest. Compound Interest is the interest earned on the interest of previous year and the initial principal.

Compound interest is calculated as follows

Amount to be received after n years = P (1 + r)n

Generally compounding is done for the following number of times –

i. For 1 month = Compounded monthly

ii. For 12 months = Compounded annually

iii. At an interval of 3 months = Compounded quarterly

iv. For 6 months = Compounded half yearly

v. For 1 day = Compounded daily.

If compounding is done on any of the following basis (except annually), the formula for calculating interest rate based on number of time compounding is done would be as follows –

3. Effective Rate of Interest – If interest is given more than one once in a year (say x times) then the effective rate of interest is calculated as follows –

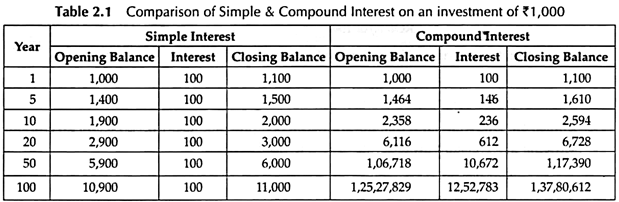
Comparison of Simple and Compound Interest:

Money is invested at Compound Interest means that each interest payment is reinvested to earn further interest in future periods. But no interest is earned on interest, the investment earns only Simple Interest.

How an investment of Rs. 1,000 grows over time under Simple and Compound Interest as to rate of interest is shown in Table 2.1 –

Time Value of Money – Theory of Interest (With Equation)

Since money has a time value, a finance manager needs a method of determining whether a cash outlay made now in an investment project can be justified in terms of expected cash inflows from the project in future years.

In other words, he must have a means of expressing future cash inflows in present rupee terms, so that the future receipts can be compared on an equivalent basis with whatever investment is required in the project under consideration. The theory of interest provides the management with the device of making such a comparison.

If a bank pays Rs.105 one year from now in return for a deposit of Rs.100 now, we would say that the bank is paying interest at an annual rate of 5 per cent. The relationship involved in this notion can be expressed in mathematical terms by means of the following equation –

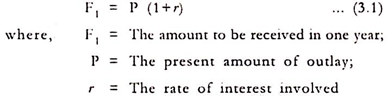
Time Value of Money – Practical Applications

The Practical Applications of Time Value of Money are:

Application # 1. Sinking Fund

Sometimes a financial manager is faced with a decision to collect a specified sum on a periodic basis at a specified rate to reach a prescribed target amount. For example, a financial manager has a target to have a sum of Rs. 1,00,000 after ten years.

Now the question arises that if a compound rate of 10% is available then what amount shall be allocated or provisioned every year so that at the end of 10th year, the finance manager would have Rs. 1,00,000 available with him.

This kind of situation normally arises in case of redemption of debentures. For example, if a company has to redeem its debenture after 5 years for which it requires Rs. 5,00,000.

Now the manager will have to work out the amount which shall be retained out of the profits of the company every year and invested at a specified rate on compounding basis so that after 5 years it shall have the target amount of Rs. 5,00,000.

This can be worked out using the formula given below:

In the above example, if we assume that the rate of interest is 8%, then annuity amount would be given as:

Application # 2. Amortization of Loan or Capital Recovery

When a firm takes loan from financial institutions, it may be required to pay the same in form of specified periodical instalments. In order to determine the size of instalments, the financial manager may use the under-mentioned formula provided the rate of lending is. known to the financial manager.

For example, A company borrows a loan of Rs. 5,00,000 which is to be repaid in form of five equal installments.

Now if the given compounding rate is 12%, the amount of each installment would be given as:

Application # 3. Case of Deferred Payment

Sometimes there is a gap of certain years between the date of borrowing and date of commencement of repayment of interest. This is known as deferred payment. For example, in the above case if the repayment of interest process is started after two years of raising the loan, then the amount to be refunded in the form of interest will be

5,00,000 (1 + 12%)2 = 5,00,000 x 1.254 = 627,000

Now for the purpose of calculating annual amount of installment, the amount of loan would be considered as Rs. 627,000

Annual amount of instalment = 627,000/3.605

Annual amount of instalment = 173,925.10

Example 14 : Vijay borrows from Kings Bank an amount of Rs. 10,00,000 @ 12% p.a. on 01.04.2012. As per agreement, repayment including interest is to be made in five equal annual instalments with first instalment falling due after three years i.e. on 31.03,2015. What would be the amount of each instalment? [D.U. B.Com, 2012]

Solution : First we shall calculate future value of Rs. 10,00,000 @ 12% after two years as shown below:

FV = 10,00,000 (l + 12%)2 = Rs/ 12,54,000

Now this will become amount of loan and the size of installment will be calculated as under:

12,54,000 = A x 3.605 A = 12,54,000 / 3.605 = Rs. 3,47,850

Application # 4. Determination of Implicit Rate of Return

Sometimes various schemes are offered by finance companies under which a person is required to deposit a specific sum in the beginning of a period and then return is available to him in the form of annuity for a certain number of years.

The investor would like to calculate the rate of interest available to him in case of such scheme for which the following formula can be used

PV = Annuity amount x PV AF (r, n)

For example, Rs. 20,000 is deposited or invested today and against this the investor is being offered an annuity of Rs. 5,000 for next five years. In this case, in order to find out the rate of interest being offered to the investor can be calculated using the above formula

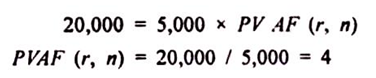
Using table A4, look for the interest corresponding to value '4' against 5th year. The interest rate is 8% (approx.) as corresponding to 5th year for 8%, the value is 3.99 i.e., closest to 4.

Time Value of Money – Timeline

Timeline is an important tool of time value of money that provides insight to the analysts about the timing and the amount of each cash flow in a cash flow stream, as depicted below.

It may be noted from Exhibit 3.1 that Time 0 is today; Time 1 is one period from today, or the end of period 1; Time 2 represents two periods from today or the end of period 2; and so on.

Cash flows shown directly below the tick marks, and interest rates are depicted directly above the timeline. Interest rate is 10 per cent for each of the three periods. Cash flows of Rs.100 made at the beginning of time 0 is an outflow (investment), shown with minus sign.

The Time 3 value is an unknown inflow and is not shown as minus sign which implies a plus sign. New cash flows occur at Times 1 and 2.

Time Value of Money – Annuity: Meaning, Types and Methods for Calculation The Present Value of Annuity

Equal series of Cash Flow either receipt or payment for a definite time period at regular intervals is known as an Annuity. Generally, Cash Flows relating to financial decisions are not equal, but when the Cash Flows are equal and constant over time it is termed as Annuity.

An Annuity is a contract whereby a financial product is sold by a financial institution which in turn accepts and promises to grow the product with an objective to make a series of equal payments to the individual upon annuitisation, at a later date.

Annuity is a fixed and equal amount of money receivable or payable (Cash Flows) at periodic intervals evenly spaced over time, usually, a year is referred to as Annuity.

Some of the common examples of Annuity products are insurance premium payments, retirement savings, mortgage payments, etc. The prime sellers of Annuity products are life insurance companies and investment companies. The most commonly used Annuity product is the insurance product.

Usually four parties are involved in an Annuity contract, which are annuitant, contract owner, beneficiary and insurance carrier. The person who will receive the periodic payment is known as the annuitant.

The person who enters into the contract is the contract owner. The annuitant and the contract owner is usually the one and the same person. Beneficiary is the person who is entitled to receive the fund on account of death of the annuitant, and lastly, the insurance company is the insurance carrier who sold the product.

The process of conversion of an investment into an equal series of payments is known as annui­tisation. Annuities are of different types depending on different parameters such as starting time of Annuity, types of pension scheme, types of pension amount and liquidity.

The most commonly used parameters are starting time of Annuity and types of pension amount.

The different types of Annuity based on these two are as follows:

1. Deferred Annuity and Annuity Due

Deferred Annuity is the type of Annuity that begins only after the expiry of a certain period of time after the final and the last premium or instalment has been paid by the purchaser of the Annuity contract. In this type of Annuity Cash Flows occur at the end of each period.

In case of Annuity Due, Cash Flows occur at the beginning of each period. The Annuity where the Cash Flows occur at the end of each period is called an ordinary or a deferred Annuity whereas the Annuity where Cash Flows occur at the beginning of each period is called an Annuity Due.

2. Immediate Annuity

In immediate Annuity, the Cash Flow commences immediately after the payment of final purchase premium.

3. Fixed Annuity

Fixed Annuity is the type of Annuity where the Cash Flow is fixed over time despite market fluctuations. This type of Annuity is preferred by those investors who like to take minimum risk.

4. Variable Annuity

Variable Annuity is the Annuity where the return is not fixed and constant over time. It varies with market fluctuations. Usually it is preferred by those investors who like to take high risk in expectation of high return.

5. Indexed Annuity

Indexed Annuity is almost similar to variable Annuity but the only difference is that the rate of return here depends on stock market indexes such as – Sensex, Nifty, S&P 500, etc. It is not available in India.

The two main advantages of Annuity products are tax saving and assured return. Unlike advantages there are some disadvantages also such as – costly investment, penalty for early withdrawal and often the complexity to understand.

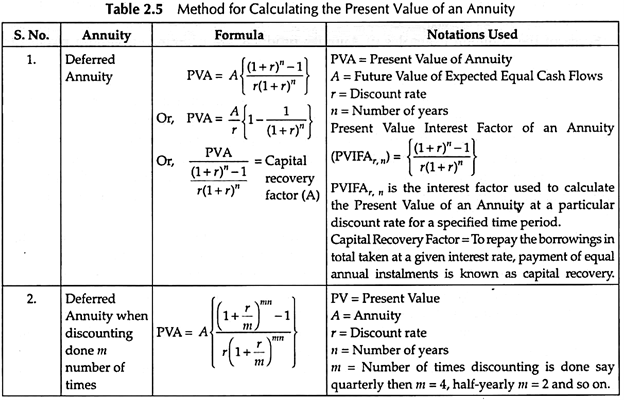
Present Value of an Annuity:

An investor may be interested in knowing the Present Value of the Annuity of his investment.

The method for calculating the Present Value of Annuity is shown in Table 2.5 –

Future Value of an Annuity:

If an investor makes an investment in an Annuity product for a specified period of time at a certain rate of interest, he may be interested in knowing the future or compounded value of an Annuity.

The method for calculating the future or compounded value of Annuity is given in Table 2.6 –

Annuity in Time Value of Money – Meaning, Example, Practical Uses and Examples

The series of payments of a given sum of money for a specific period of time is called an annuity.

For example, if we have to pay Rs. 1,000 every year for 5 years, this series of payments will be called "an annuity of Rs. 1,000 for 5 years". If we calculate the present worth of this series of 5 annual payments, it is called the present value of this annuity and if we want to know the future value after 5 years, it is called the maturity value of the annuity.

This series can be shown as follows:

The formula for calculating the present value of the annuity, without going into the detailed calculations, is as follows:

Types of Annuities:

1. Annuity Due:

In the above example, the first payment of the annuity is at the end of year 1. Such annuities are called 'Ordinary Annuities'. In some situations, however, we can have the first payment occurring at the beginning of the year, i.e. at point 0, while the last payment is at the end of year 4. Such an annuity is called 'Annuity Due'.

The series of payments in case of annuity due will be as follows:

Annuity Values with Changing Rates of Interest:

In the above illustrations, we assumed that the rate of interest remains constant during the tenure of the annuity. However, we may have some situations where the rate of interest is changing during the tenure of the annuity. In such a situation, both the present as well as the maturity values have to be adjusted for these different rates of interest.

2. Deferred Annuities:

Sometimes, we encounter deferred annuities. A deferred annuity implies that payment of annual sum or its maturity value has been postponed for some years. In such a situation if we calculate either the present value or the maturity value some adjustment has to be made for this deferment.

The payment of cash flows in a deferred annuity may be as follows:

In the above figure we find that the first payment starts after 3 years from now. In other words, it is a deferred annuity for two years. In such a situation if we have to calculate the present value of the annuity, then we treat it as an ordinary annuity, starting at year 2 and calculate its present value at point 2. Then, it is further discounted for 2 years to find its value at point '0'.

This is done as follows:

= 3790.79/ (1.1)2

= Rs. 3132.88

Sometimes, the payment of maturity value may be deferred. For example, we deposit a certain sum for 5 years but get its maturity payment 2 years after the last installment is paid.

In such a case, cash-flow payments would be as follows:

In order to calculate its value at the end of 7 years from now, we find its maturity value at the end of 5 years, treating it as an ordinary annuity and then compound this value further for 2 more years and the value is found as follows –

= 6105.10 (1.1)2

= Rs. 7387.17

Similarly, present and maturity values of 'deferred annuity dues' may also be calculated.

3. Variable Annuity:

Annuities may be variable also. For example, first year's amount is 1000 while second year's amount is 1100, for third year 1200 and so on for the given number of years. In such situations present and maturity values may have to be found.

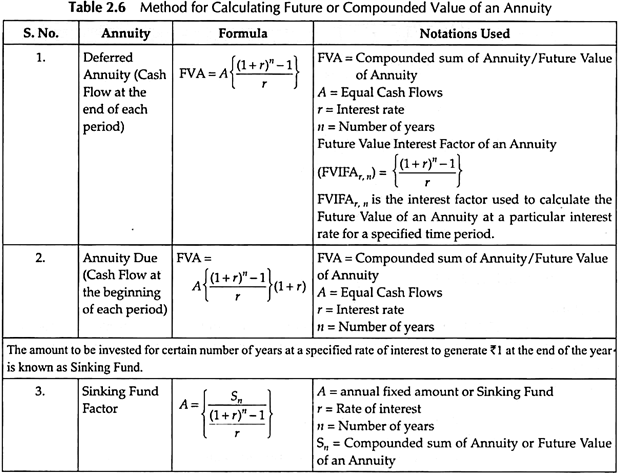
Where

a = initial amount

b = annual increment

PVF = Present Value factor of Annuity for the given rate of interest and maturity period

t = time period

i = given rate of interest.

Similarly, if we have to find the maturity value of a variable annuity, by the following formula:

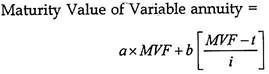
Where

MVF = Maturity Value factor for annuity for the given rate of interest and maturity period

Other symbols are as above.

Practical Uses of Annuity Principles:

The concept of time value of money or the discounting principle is of great use in our everyday life. When we purchase any consumer durable on installment, we can find the implied rate of interest charged by the seller or the financer. If we are purchasing bonds or debentures then the price to be paid can be decided by this concept.

Similarly, the maturity values of recurring deposits or insurance policies etc. can be found with the help of discounting principle. The basic rule for any such decision making is that 'no comparison can be made for payments/receipts occurring at different points of time'. They must be brought to a common point of time before any such decision can be taken.

We can illustrate it by the following example:

Suppose a refrigerator is available from a dealer for Rs. 10,000 on cash down basis. The second option is to purchase it for 3 equal annual installments of Rs. 4000 each, first installment will be made after 1 year. The question is that which option should be chosen?

Here, we see that the two options are not directly comparable because they are occurring at different points of time. We will now find the present value of 3 annual installments of Rs. 4000 each. Suppose the rate of interest is 10%.

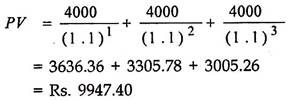
Thus, we find that the present value of installments is lower than the cash-down price and, hence, installment offers should be immediately accepted. Similarly, many such decisions can be made.

Discounting principle is of great essence in all inter­-temporal decisions e.g., investment or capital budgeting decisions.

In any investment decision, we make expenditure at present, but the benefits of that expenditure are to be received in future. The benefits cannot be compared with present expenditure because they are received at a different point of time. In order to make them comparable, we should bring them to a common point of time. In other words, we will discount the future benefits for the present at an appropriate discount rate. Then only a reasonable comparison can be made between expenses and benefits.

If the present value of benefits exceed the present value of expenses, then the particular capital expenditure is worthwhile and be accepted. If the present value of future benefits is less than the present expenditure, then, it can be concluded that the given investment or the capital expenditure is not worthwhile and will result in a net loss and, therefore, should not be undertaken.

Time Value of Money – Types of Cash Flows: Perpetuity, Annuity Due,  Growing Perpetuity and Growing Annuity

There are other types of cash flows which may be referred to as modified versions of cash flows.

These types of cash flows are discussed as under:

Type # 1. Perpetuity

A perpetuity is an infinite series of equal cash flows which occur at regular intervals but the period for which these cash flows occur is infinite. The present values of such cash flows will be given by the formula

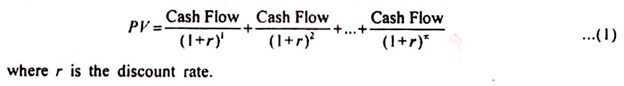
In this case, instead of having terminal cash flow at nth year, it is presumed that the cash flow occurs for an indefinite period.

Thus, the present value of a perpetuity is equal to the amount of perpetuity divided by the rate of interest.

Type # 2. Annuity Due

In the normal course, it is presumed that cash flow occurs at the end of each period. For example, when we talk of cash flow occurring in 5th year, it means that cash flow occurs at the end of the 5th year. However, in practice the cash flow may also occur in the beginning of the specified period. Such cash flows are known as annuity due.

For example, in the above case the cash flow relating to 5th year, if happens to be annuity due, shall occur at the beginning of the 5th year. Thus, in both the cases there would be the same number of cash flows. However, in case of annuity due, the first cash flow occurs now whereas terminal cash flow occurs at the beginning of terminal year.

It means that the cash flow in case of annuity due precedes the cash flows in the normal course by a unit period. If the cash flows are of yearly nature and the discount rate being used is V then the relationship between the two would be given as :

Using this relationship the future value and the present value of an annuity due will be given by the formulae given below

Type # 3. Growing Perpetuity

In case of perpetuity, a series of cash flow of equal amount takes place at periodic intervals for an infinite period. But, in case of growing perpetuity, a series of cash flows of different amounts takes place at periodic intervals for an infinite period. Though the amounts are different but there is a specific relation between them.

The cash flow of nth period is greater than the cash flow of (n +1)th period. There is a periodic cash flow which grows at a constant rate. For example, the cash flows at time t1, t2, and t3 of amounts 100, 110 and 121 respectively will be said to be growing perpetuity because cash flow of (n + 1)th period is greater than cash flow of nth period by 10%.

The present value of cash flows increasing at the growth rate 'g' discounted at rate V is given by the formula

Type # 4. Growing Annuity

It is a finite series of equal and periodic cash flow growing at a constant rate every period. Thus, growing annuity may be considered as a combination of growing perpetuity. The present value of growing annuity may be given as

where CF(1) = cash flow at the end of the period

r = Rate of Interest

g = growth rate

n = size of an annuity

Time Value of Money – Risk: Meaning, Types and Measurement (with Formulas)

Meaning

The business dictionary defines risk as exposure to the possibility of loss, injury, or other adverse or unwelcome circumstance, i.e., a chance or situation involving such a possibility. Risk is the probability or possibility of having a negative outcome due to certain sudden events.

The variation of the actual outcome from the expected outcome is defined as risk. In simple terms, risk is the volatility in actual outcome. It is a sudden occurrence of some unexpected or unplanned events resulting in reduction of earnings or huge financial losses.

Although used synonymously, risk is a bit different from uncertainty. In case of risk, proba­bilities of the occurrence of an event can be predicted based on the past available facts, figures and information for the purpose of decision making, but in case of uncertainty the occurrence of an event cannot be predicted, due to unavailability of facts, figures and information.

Uncer­tainty varies from zero (0) to infinity (∞). Risk is better than uncertainty. Risk lies somewhere between certainty and uncertainty. If uncertainty is equal to 0, it indicates certainty.

Types of Risk:

Risk can be categorised into three broad categories—

1. Business Risk,

2. Non-Business Risk, and

3. Financial Risk.

Business Risk is the risk associated with the day-to-day activities of business or the operational activities of the business. It depends on certain factors such as – changes in demand, input prices and obsolescence due to technological advances.

Non-Business Risk refers to all forms of risk that are beyond the control of any business. Political risk and all sorts of risk associated with variation in macroeconomic factors fall under this category of risk.

Financial Risk is the most common form of risk. This form of risk is associated with the financing decision of a firm. It is a major area of concern for all the firms. Financial Risk is associated with a host of factors such as – the uncertainty in the movement of the market due to factors such as fluctuation in interest rate, currencies and stock/share prices caused by certain macro and micro factors.

Financial Risk can be further classified into following types—

1. Market risk,

2. Credit risk,

3. Liquidity risk,

4. Operational risk and

5. Legal risk.

Market Risk is associated with uncertain movement of stock prices, credit risk refers to the risk when one party generally the customer-taken credit fails to fulfil the commitment, liquidity risk refers to risk that an asset may not be sold in the market quickly for realisation of cash in time of financial crunch, operational risk is associated with the possibility of failure of business due to mismanagement, human errors or some technical reasons and legal risk refers to the financial losses due to huge legal constraints.

Broadly, risk can also be of the following types—investment risk, systematic risk, unsys­tematic risk and portfolio risk. Investment Risk is the risk associated with an Investment Decision. This type of risk arises when the expected return is less than the actual return. Systematic Risk is also known as uncontrollable risk or diversifiable risk. This type of risk is beyond the control of a firm.

This risk arises due to change in macroeconomic factors such as – currency fluctuation, inflation, changes in economic policy, etc. Unsystematic Risk is also known as the controllable risk or the non-diversifiable risk. This type of risk is specific to a company which is due to certain factors such as paucity of funds, resources, human capital, huge litigations, etc.

Portfolio Risk is the risk which arises due to investment in different projects to minimise the risk portfolio investment is made. This risk cannot be eliminated in total but can be minimised.

Measurement of Risk:

There are various methods of measuring risk.

The following will provide an overview of the different methods available:

1. Sensitivity Analysis:

It is a method of risk estimation based on the decision model. Under this approach, the probable impact of risk arising due to change in the data set is tried to be assessed on the decision model. It measures the sensitivity of the data set used for decision making, i.e., trying to assess the changes in expected values or outcomes of a decision model due to change in the data set.

Analysing the sensitivity of the data set which is very vital for decision making ensures better decision making of the management of a firm. So this technique does not measure risk in quantitative terms but rather in qualitative terms by stating the impact on the final decisions due to sudden variations in those factors affecting decision making.

2. Probability Distribution and Expected Values:

Probability is the chance of occurrence of an event. Probability distribution not only takes into account the possible or expected return from each alternative but also considers the uncertainty associated with each of the alternatives. Probability can be objective or subjective.

Objective probability is based on a large number of observations under independent and identical situations, whereas subjective probability is totally based on individual judgement or decision and not based on a large number of identical and independent observations.

3. Standard Deviation:

Standard Deviation is an absolute measure of dispersion. Dispersion is variation of the actual value from the central value or mean. Standard Deviation measures the deviation of actual return from the expected return in absolute terms. It is the positive square root of the mean of the squares of the deviations of the variables from their arithmetic mean. It is denoted by sigma (σ).

High Standard Deviation indicates higher dispersion, i.e., higher amount of risk, whereas low Standard Deviation reveals lower dispersion, i.e. lower amount of risk.

Standard deviation is expressed by the following formulae:

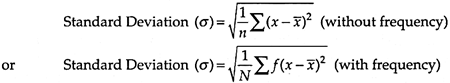
Standard Deviation is not a reliable measure of risk; this measure suffers from the limitation that in case of a project involving different Cash Outflows and different expected returns or mean values, this measurement of risk has the high chance of giving misleading results. So it is not suitable for comparison.

Coefficient of Variation:

Coefficient of variation is a relative measure of risk. It is expressed as –

This is measured as Standard Deviation as percentage of mean. This method is also not a reliable measure of risk but it helps in comparison in case of projects having different Cash Outflows and different expected returns. Higher coefficient of variation reveals higher degree of risk and vice versa.

4. Decision Tree Analysis:

In this method, the decision tree is drawn to explain the full set of prob­able events and alternatives that may arise under a given situation. Each course of action is represented by a branch which further has subsidiary branches which represents the prob­able alternative course of actions and events in future.

In case of an Investment Decision, this Decision Tree Analysis method is usually followed, where the Investment Decision is portrayed by a tree along with branches which represents the future probable events.

5. Capital Asset Pricing Model:

Capital Asset Pricing Model (CAPM) measures the ex­pected return on equity. In this method, the return on equity has two components—one is the risk-free rate of return and another is the risk premium.

Risk-free rate of return is the assured return especially on the government or the gilt-edged securities. Risk pre­mium is the additional or extra return for investing in a particular risky security.

Risk premium component comprises average return on the market portfolio and the beta factor which represents the risk of a particular security. Beta measures sensitivity of an investment in respect to the market.

It is measured as follows:

Beta value (β) > 1, represents high-risk security, beta value (β) < 1 represents low-risk securities and beta (β) = 1 represents neutral, i.e., neither high risk nor low risk.

6. Alpha:

It is also another measure of risk, where risk is measured relative to the market risk or the benchmark index.

7. R squared (R 2 ):

This measure is expressed as a percentage (%) of a particular investment's or security's movement in terms of the movement of the benchmark index.

8. Sharpe Ratio:

This ratio is calculated to determine whether the return arising from an investment is due to rational Investment Decision or the reward for taking excess or high risk.

Time Value of Money – Return: Meaning and Measurement (with Formulas)

Return is simply, the Cash Inflows arising from an investment. Return arising from an investment has two components, one the periodic return called the dividend or interest on the principal sum invested and another the difference between the price at the time of investment, i.e., purchase price and the ending, i.e., the selling price.

Periodic return may be received in different ways such as – annually, bi-annually, quarterly, etc. From a business point of view return is the reward of a business for carrying out its operation and undertaking risk involved in such operations. From an investor's point of view, the perception of return varies from investor to investor.

Some may opt for high returns on a short-term basis, whereas others may like to invest in long-term growth funds. Again, some may like to invest in the security of a company with sustainable growth in sales and earnings over the years, whereas some may invest in the security of a company based on its high return on net worth.

Measurement of Return:

Some of the commonly used techniques of return measurement are as follows:

1. Return on Investment (ROI):

ROI is the profit earned by a company in relation to the amount of capital invested. It is the measure which indicates the overall financial performance of a company. Return on Investment as a measure of return was first developed by DuPont Company in USA in the year 1919.

It is expressed as follows:

High ROI, indicates higher return whereas low ROI represents low return. This ratio has certain advantages such as it measures the Operating Profit of a firm, helps in understanding the profit earning capacity of a firm, indicates efficiency of assets utilisation, helps in taking long-term Investment Decision but at the same time suffers from some limitations such as – unsuitable for short-term Investment Decisions, perception of profit varies, etc.

2. Internal Rate of Return (IRR):

It is that rate of return at which Present Value of Cash Inflow is just equal to the Present Value of the Cash Outflow, i.e., the initial cost of investment, which means at IRR, the Net Present Value, i.e., Present Value of Cash Inflow—Present Value of Cash Outflow is just equal to zero. It is also known as the opportunity Cost of Capital.

Internal Rate of Return is calculated as:

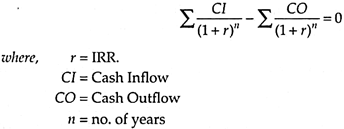
Under this method, an Investment Decision is taken based on criteria for a single project as r (rate of return) > K (Cost of Capital), accept the project; r (rate of return) < K (Cost of Capital), reject the project; and r (rate of return) = K (Cost of Capital), firm is indifferent.

In case of mutually exclusive projects, the project with higher IRR is to be selected. This method as an Investment Decision measure has certain advantages such as – it considers the Time Value of Money factor, Cash Inflows are taken in total for estimated life, easy to understand, does not takes into account the Cost of Capital in its calculation, etc., whereas at the same time it suffers from various limitations such as – involving very complex calculation, difficulty in decision making in case of mutually exclusive project, ignores the concept of Cost of Capital or the required rate of return, etc.

3. Weighted Average Cost of Capital:

Cost of Capital is the minimum or the required rate of return to be earned on a project to retain the investors. Weighted average Cost of Capital is calculated as the Cost of Capital of individual sources multiplied by the respective weights and their sum divided by the total of their weights.

4. Weighted Average Return Method:

Under this method, similarly, the returns from different projects are calculated and that figures are multiplied by their respective weights. Finally, the sum of the product is divided from the total of their weights. The potential income from a particular investment varies from one investment to another. This potential income from different investments is called the weight of an investment. Such potentialities may be high, low or moderate.

5. Profit Method:

This is a simple method of return estimation. In this method, profit that is calculated by deducting the amount of purchase from the sales amount is taken to be the return.

6. Cash Flow Method:

Under this method, Cash Outflows are deducted from the Cash Inflows of a project. Only cash items are considered. The difference between Cash Inflows and Cash Outflows is known as the return from a project.

7. Income Method:

Under this method, return is the income which is the excess of total revenue over and above the total expense. There are different types of income such as – income before interest and tax, income before tax and after tax, etc.

8. Ratio Analysis Method:

Ratio depicts the relationship between two variables in the financial statements. For example, if we calculate the gross profit ratio as (Gross Profit / Sales) x 100, it measures the return by deducting the cost of goods sold from the sales figure, i.e., gross profit—measuring it as a percentage of sales.

Again if we take return on capital employed, it is the net earnings of a firm as percentage of the capital employed, or all these are the commonly used measures of return.

Time Value Money – Time Value Factors (TVFS)

Time Value factor is the value of a rupee at a given percent of TPR, for a given period of time.

There are two types of TVFs, namely- Compound /Future Value factor and Present Value factor.

(a) Present Value factor (PVF) or discount factor (DF) is the value of a rupee today at a certain rate of return or at interest rate for the given period of time.

(b) Compound Value factor/Future Value factor is the value of a rupee at a certain rate of interest for the given future period of time.

Symbolically, CVF or FVF = (1 + i)

Time Value Money – Capital Asset Pricing Model: Meaning, Equation and Assumptions of CAPM

Capital Asset Pricing Model:

The capital asset pricing model (CAPM) attempts to measure the risk of a security in the portfolio sense. It considers the required rate of return of a security on the basis of its contribution to total portfolio risk. The core idea of the CAPM is that only undiversified risk is relevant to the determination of expected return on any assets.

Since the diversifiable risk can be eliminated, there is no reward for it. In fact, the CAPM can be used to examine the risk and return of any type of capital assets such as individual security, an investment project, or a portfolio of assets/ investment.

The CAPM can be expressed as follows:

The equation of CAPM, thus says that the expected return of a portfolio should exceed the risk free rate of return by an amount i.e., proportional to the beta factor to the investor.

Assumptions of CAPM:

The CAPM is based upon several assumptions as follows:

1) The investors are basically risk averse.

2) All investors want to maximize the wealth and therefore choose a portfolio solely on the basis of risk and return assessment.

3) All investors can borrow or lend an unlimited amount of funds at risk free rate of interest.

4) All investors have identical estimates of risk and return.

5) All securities are perfectly divisible and liquid and there is no transaction cost.

6) All investors are efficiently diversified and have eliminated the unsystematic risk.

Time Value of Money – Time Preference Rate (TPR)

Time preference rate of money can be expressed as an interest rate. Interest rate gives money its value, and facilitates the comparison of cash flows occurring at different time periods.

The minimum interest rate in the absence of any risk is known as risk-free rate. It is a compensation for time. If an individual is exposed to some degree of risk, he would expect a rate of return higher than the risk-free rate from the investment compensating him for both time and risk. The rate added to compensate risk is known as risk premium.

The interest rate permits the individual to convert different amounts offered at different times to amounts of equivalent value in the present, i.e., a common point of reference for decision.

The time value of money depends on 'rate of return or rate of interest earned' by investing or lending of funds. By using this, we can find out the present value of future sum of money and/ or future value for present sum of money.

Time preference rate is used to translate the different amounts received at different time periods; to amounts equivalent in value to the firm/individual in the present at common point reference. This time preference rate is normally expressed in 'percent' to find out the value of money at present or in future.

Time Value of Money – Multiple Choice Questions and Answers

1. Time value of money indicates that

(a) A unit of money obtained today is worth more than a unit of money obtained future

(b) A unit of money obtained today is worth more less than a unit of money obtained future

(c) There is no difference in the value of money obtained today and future

(d) None of the above

Ans (a)

2. Time value of money supports the comparison of cash flows recorded at different time periods by

(a) Discounting all cash flows to a common point of time

(b) Compounding all cash flows to a common point of time

(c) Using either (a) or (b)

(d) None of the above

Ans (c)

3. In time value of money, nominal rate is

(a) Not shown on timeline

(b) Shown on timeline

(c) Multiplied on timeline

(d) Divided on timeline

Ans (a)

4. In calculation of time value of money, PMT represents

(a) Present money tracking

(b) Payment

(c) Payment money tracking

(d) Future money payment

Ans (b)

5. Discounted cash flow analysis is also classified as

(a) Time value of stock

(b) Time value of money

(c) Time value of bonds

(d) Time value of treasury bonds

Ans (b)

6. Time value of money is an important finance concept because

(a) It takes risk into account

(b) It takes time into account

(c) It takes compound interest into account

(d) All of the above

Ans (d)

7. In calculating time value of money, N represents

(a) . Number of payments periods

(b) Number of investments

(c) Number of installments

(d) Number of premium received

Ans (a)

8. Process of calculating future value of money from present value is classified as

(a) Compounding

(b) Discounting

(c) Money value

(d) Stock value

Ans (a)

9. Type of interest rates consists of

(a) Nominal rates

(b) Periodic rates

(c) Effective annual rates

(d) All of the above

Ans (d)

10. Future value of interest if it is calculated once a year is classified as

(a) One time compounding

(b) Annual compounding

(c) Semi-Annual compounding

(d) Monthly compounding

Ans (b)

11. Payments if is made at the end of each period such as on the end of year is classified as

(a) Ordinary annuity

(b) Deferred annuity

(c) Annuity due

(d) Both (a) and (b)

Ans (d)

12. An interest rate which is paid by money borrower and charged by lender is considered as

(a) Annual rate

(b) Periodic rate

(c) Perpetuity rate of return

(d) Annuity rate of return

Ans (b)

13. An interest rate which is quoted by brokers, banks and other financial institutions is classified as

(a) Annuity rate

(b) Perpetuity rate

(c) Nominal rate

(d) External rate of return

Ans (c)

14. An annuity is

(a) More than one payment

(b) A series of unequal but consecutive payments

(c) A series of equal but consecutive payments

(d) A series of equal but non-consecutive payments

Ans (c)

15. A type of security payment in which payments are made at equal intervals of time and each payment amount is same is classified as

(a) Fixed interval investment

(b) Fixed payment investment

(c) Annuity

(d) Lump Sum amount

Ans (c)

16. If payment of security is paid as Rs. 100 at the end of year for 3 years, it is an example of

(a) Fixed payment investment

(b) Lump Sum amount

(c) Fixed interval investment

(d) Annuity

Ans (d)

17. An annuity with an extended life is classified as

(a) Extended life

(b) Perpetuity

(c) Deferred Perpetuity

(d) Due Perpetuity

Ans (b)

18. The future value of an annuity is

(a) More than each annuity payment

(b) Less than each annuity payment

(c) Equal to each annuity payment

(d) None of the above

Ans (a)

19. Prices of bonds will decrease if an interest rate

(a) Rises

(b) Declines

(c) Equals

(d) None of the above

Ans (a)

20. Future value of interest if it is calculated two times a year is classified as

(a) Semi- annual discounting

(b) Annual compounding

(c) Semi- Annual compounding

(d) Annual discounting

Ans (c)

21. Periodic rate if it is multiplied with per year, number of compounding periods is called

(a) Extrinsic rate of return

(b) Intrinsic rate of return

(c) Annual rate of return

(d) Nominal rate of return

Ans (d)

22. Heterogeneous cash flows can be made comparable by

(a) Discounting technique

(b) Compounding technique

(c) Either (a) or (b)

(d) None of the above

Ans (c)

23. Both the future and present value of a sum of money are based on

(a) Interest rate

(b) Number of time periods

(c) Both (a) and (b)

(d) None of the above

Ans (c)

24. The present value of a rupee to be received in the future is

(a) More than a rupee

(b) Less than a rupee

(c) Equal to a rupee

(d) None of the above

Ans (b)

25. The future value of a rupee that you invest today is

(a) More than a rupee

(b) Less than a rupee

(c) Equal to a rupee

(d) None of the above

Ans (a)

26. The concepts of present value and future value are

(a) Directly related to each other

(b) Not related to each other

(c) Proportionally related to each other

(d) Inversely related to each other

Ans (d)

27. Finance company provides loans at 12% with 2 compounding periods per year, periodic rate is classified as

(a) 3% per quarter

(b) 6% per quarter

(c) 6% per year

(d) 0.1667% per year

Ans (c)

28. An interest rate is 5%, number of period are 3 and present value is Rs. 100 and then future value will be

(a) 115.76

(b) 105.00

(c) 110.25

(d) 113.56

Ans (a)

29. If security pays Rs.5,000 in 20 years with 7% annual interest rate, PV of security by using formula is

(a) Rs.1290.10

(b) Rs.1292.10

(c) Rs.1,295.10

(d) Rs.1297.10

Ans (b)

30. Securities future value is Rs. 1,00,000 and present value of securities is Rs.5,00,000 with an interest rate of 4.5%, N will be

(a) 16.7473 years

(b) 0.0304 months

(c) 15.7473 years

(d) 0.7575 years

Ans (a)

31. Security present value is Rs.100 and future value is Rs.150 after 10 years and value if 1 = interest rate will be

(a) 4.14%

(b) 0.59%

(c) 0.69%

(d) 0.79%

Ans (a)

32. If the nominal rate of interest is 10% per annum and there is quarterly compounding, the effective rate of interest will be

(a) 10% per annum

(b) 10.10% per annum

(c) 10.25 % per annum

(d) 10.38% per annum

Ans (d)

33. If the nominal rate of interest is 10% per annum and annual effective rate of interest is 10.25% per annum, determine the frequency of compounding

(a) 1

(b) 2

(c) 3

(d) None of the above

Ans (b)

34. Value of payment is Rs.25 and an interest rate is 2% then the present value will be

(a) Rs.12.54

(b) Rs.12,500.00

(c) Rs.12,504.00

(d) Rs.8,400

Ans (c)

35. Future value of annuity is if deposited value id Rs.100 and earn 5% every year of total 3 years will be

(a) Rs.315.25

(b) Rs.331.01

(c) Rs.99.49

(d) Rs.318.25

Ans (a)

36. If deposited money is Rs. 10,000 in bank pays interest 10% annually, an amount after 5 years will be

(a) Rs. 16,105.14

(b) Rs. 16,110.14

(c) Rs. 16,115.14

(d) Rs. 16,505.14

Ans (a)

Importance Of Time Value Of Money

Source: https://www.economicsdiscussion.net/financial-management/time-value-of-money/32809

Posted by: wickershambetwou61.blogspot.com

Share this post